Discontinuous Galerkin On Graphics Processing Units

Discontinuous Galerkin (DG) is a popular class of numerical methods for solving partial differential equations (PDEs). Like any other finite element method, the solution inside each mesh element is approximated by a set of basis functions in DG. However, as indicated by the name, no continuity restrictions are enforced at element interfaces. The coupling between adjacent elements only comes in with uniquely defined inter-element numerical fluxes. The discontinuity nature might be counterintuitive at first glance, while it buys DG many advantages over traditional numerical methods.

From the perspective of parallelization, the computing and memory access pattern in DG is mostly local and hence are generally easy to parallelize. Moreover, the high-order solution representation requires less data points (degrees of freedom) to resolve the physics and thus less memory access compared to finite volume and finite difference methods, though with the expense of higher arithmetic intensity per degree of freedom. The relatively high computation intensity and low memory access make DG particularly suitable for parallelization on Graphics Processing Units (GPUs).

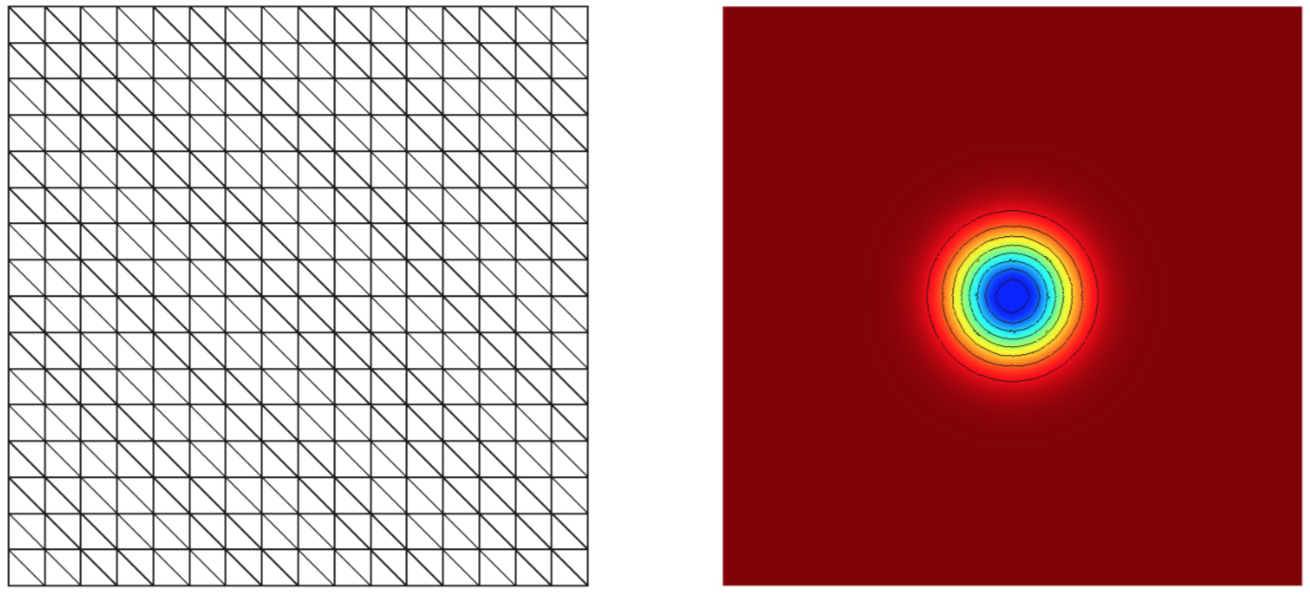
In this blog, I’ll present a simple DG implementation on GPU using the Compute Unified Device Architecture (CUDA) programming model. The problem of interest is the inviscid vortex transport in a square domain, with periodic boundaries. Figure 1 shows a sample computational mesh and the initial pressure field.

Governing Equations

Discretization

Implementation

Experiments and Performance Analysis

Here are the animations of the simulation on GPU for the vortex transport problem.

More details about the implementations and the scaling performance can be found in this short report and the codes can be found on my Github repository.